what is Bayes' theorem#
贝叶斯推断(Bayesian inference)是一种统计学方法,用来估计统计量的某种性质。
它是 贝叶斯定理(Bayes' theorem)的应用。英国数学家托马斯·贝叶斯(Thomas Bayes)在1763年发表的一篇论文中,首先提出了这个定理。
Bayesian inference 与其他统计学推断方法截然不同。它建立在主观判断的基础上,也就是说,你可以不需要客观证据,先估计一个值,然后根据实际结果不断修正。正是因为它的主观性太强,曾经遭到许多统计学家的诟病。
贝叶斯推断需要 大量的计算,因此历史上很长一段时间,无法得到广泛应用。只有计算机诞生以后,它才获得真正的重视。人们发现,许多统计量是无法事先进行客观判断的,而互联网时代出现的大型数据集,再加上高速运算能力,为验证这些统计量提供了方便,也为应用贝叶斯推断创造了条件,它的威力正在日益显现。
贝叶斯定理#
贝叶斯定理, 实际上就是计算 条件概率的公式。
所谓"条件概率"(Conditional probability),就是指在事件B发生的情况下,事件A发生的概率,用\(P(A|B)\)来表示。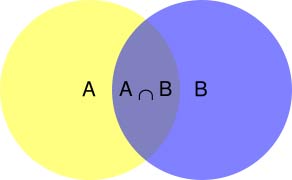
根据文氏图,可以很清楚地看到 \(P(A|B)\) 就是 \(P(A \cap B)\)除以\(P(B)\)。 \[P(A|B) = \frac {P(A \cap B)} {P(B)}\] 即: \[P(A \cap B) = P(A|B) P(B)\] 同理: \[P(A \cap B) = P(B|A) P(A)\] 因此: \[P(A|B) = \frac {P(B|A) P(A)} {P(B)}\]
我们把 \(P(A)\)称为先验概率(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。\(P(A|B)\)称为后验概率(Posterior probability),即在B事件发生之后,对A事件概率的重新评估。\(\frac{P(B|A)}{P(B)}\) 称为似然函数(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解成下面的式子:
1
后验概率 = 先验概率 x 调整因子
when to use Bayes' theorem#
我们先看看简单的例子: - 事实 Evidence: Robin个性安静,喜欢阅读。
需要猜测 Robin是图书管理员 还是 农民。大多数人也许会认为Robin是图书管理员。 - 假设 hypothesis: Robin是图书管理员
接下里我们验证一下这个概率,其中目前数据显示: - 人群中: 图书管理员/农民 = \(\frac{1}{20}\) - 图书管理员符合Evidence的概率为 \(\frac{4}{10}\) - 农民符合Evidence的概率为 \(\frac{1}{20}\)
我们需要求出: P(H|E) - P(H|E) --> P(hypothesis given evidence):后验概率,指Evidence条件下,hypothesis成立的概率。通俗的讲,\(P(H|E) = \frac{H中符合E的概率}{符合E的总概率} = \frac{P(E|H) P(H)}{P(E)}\)
\(P(E|H) = \frac{4}{10}\) :P(evidence given hypothesis) Likehood 似然,这里指 图书管理员 中 符合Evidence 的概率。
\(P(H) = \frac{1}{1+20} = \frac{1}{21}\) 。\(P(H)\)也叫 先验,这里指图书管理员的概率。
\(P(E) = \frac{4}{10} + \frac{1}{20} = \frac{9}{20}\)
所以 $P(H|E) = {P(E)} = {} $
reference#
1.Bayesian inference 2.Bayes' theorem 3.贝叶斯推断及其互联网应用(一):定理简介