LiuWen's Blogs
0%

[数据结构]1.树状数组 Binary Indexed Tree

Posted on Edited on In

1.what can Binary Indexed Tree do？#

树状数组，也称作“二叉索引树”（Binary Indexed Trees）或 Fenwick Tree。 它可以高效地实现如下两个操作： 1. 数组前缀和（prefix sum)的查询 2. 单点更新(update)

2.why choose Binary Indexed Tree?#

假设有个n维数组： [2,3,5,-1,6] query(2,4) 求从第二个元素到第四个元素的和: 3 + 5 - 1 = 7 update(4, 2): 更新第四个元素加2

  • 普通遍历法： query: O(n) update: O(1)

  • dp 方法 建立prefix sums数组(前i个元素的和) 耗时: O(n); query: O(1) 如果有个元素需要更新,则需要更新所有涉及的 prefix sums数组元素:O(n)

  • 树状数组 每个结点仅 存储部分元素的和 query: O(log(n)) update: O(log(n))

3.Basic idea of Binary Indexed Tree#

Binary Indexed Tree的 每个结点仅 存储部分区间元素的和. 我们以长度为16的数组为例

-- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
A数组 1 0 2 1 1 3 0 4 2 5 2 2 3 1 0 2
C数组 1 1 3 4 5 8 8 12 14 19 21 23 26 27 27 29
tree node include range 1 1~2 3 1~4 5 5~6 7 1~8 9 9~10 11 9~12 13 13~14 15 1~16
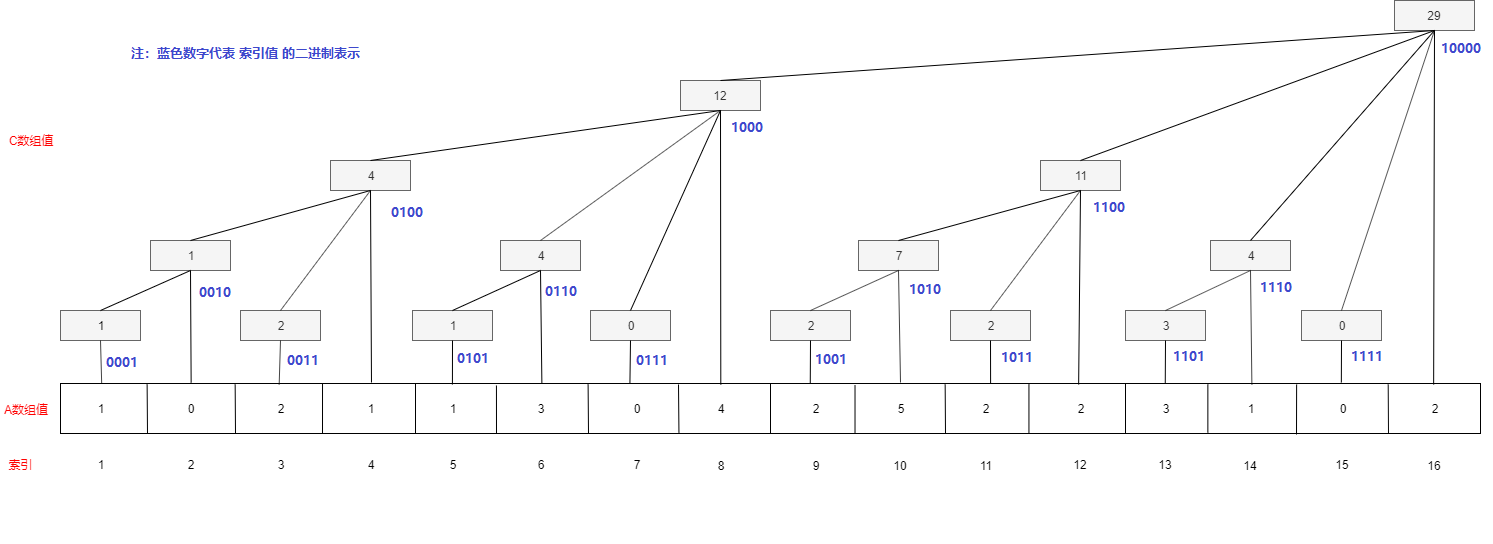
  • A数组是 原值, C数组是 根据某一规则存的是A数组若干项的和。
  • 从上图来看，C数组似乎是呈对称的形态，比如C[8]表示A[1] ~ A[8]的和，而C[4]表示A[1] ~ A[4]的和，所以C[8]又可以表示C[4] + [6] + C[7]。一个C数组的元素只有一个父结点，但却有好多子节点，可以形象地理解为一个C数组元素管着一片区域，怎么去知道一个元素到底在管着哪些A数组的元素呢？ 下面是C[1] ~ c[8]值计算方式： 
    1
    2
    3
    4
    5
    6
    7
    8
    C[1] = A[1];
    C[2] = A[1] + A[2];
    C[3] = A[3];
    C[4] = A[1] + A[2] + A[3] + A[4];
    C[5] = A[5];
    C[6] = A[5] + A[6];
    C[7] = A[7];
    C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];
    我们把上面索引的十进制，全部换成二进制，如下： 
    1
    2
    3
    4
    5
    6
    7
    8
    C[1] = C[0001] = A[0001];
    C[2] = C[0010] = A[0001]+A[0010];
    C[3] = C[0011] = A[0011];
    C[4] = C[0100] = A[0001]+A[0010]+A[0011]+A[0100];
    C[5] = C[0101] = A[0101];
    C[6] = C[0110] = A[0101]+A[0110];
    C[7] = C[0111] = A[0111];
    C[8] = C[1000] = A[0001]+A[0010]+A[0011]+A[0100]+A[0101]+A[0110]+A[0111]+A[1000];
    仔细观察上面的二进制表示，我们可以发现，\(C[i]\)管的范围就是 \(i\) 的二进制表示数 从低位到高位第一个为1的位置，(高位保持不变)和其所有低位二进制元素之和。

3.1 lowbit#

那么怎么知道从低位起第一个为1的数怎么表示？这个操作有个名字叫做lowbit，计算方式为: 

1
lowbit(i) = i & (-i)
计算该数的二进制从右往左第一个非0位所表示的10进制数，如下所示： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
* (二进制)保留最低位的1及其后面的0，高位的1全部变为0，
* 即得到该数的二进制从右往左第一个非0位所表示的10进制数。
* 例如：
* <pre>
*  原值 0000 0110
*  取反 1111 1001
*  +1  1111 1010
*  & 0000 0010
* </pre>
*
* @param k 待处理的十进制数
* @return 处理后的十进制数
*/
private static int lowBit(int k) {
    return k & -k;
}
再从图片宏观来看，我们发现整个结构似乎有点 二分的味道，具有某种对称性。 - 如果数组位置是奇数，那么\(C[i] = A[i]\)； - 如果是偶数，可以形象地看作二分：\(C[i] = C[i / 2] + A[i - (i / 2) + 1] + .... + A[i]\)。 而\(C[i / 2]\)又可以利用上面的二分继续继续进行分割，直至不可分割。上面可以推导出如下公式：\(C[i]=A[i−2k+1]+A[i−2k+2]+…+A[i]\) ，其中k为i的二进制中从最低位到高位连续零的长度。其中这个2k就是上面提到的\(lowbit(i)\)。所以我们就知道即C[i]数组中保存的就是数组A的区间\([i-lowbit(i)+1, i]\)中所有数的和，公式如下：

\[ C[i] = \sum_{n=i-lowbit(i)+1}^i A[i]\]

除此之外，还有一些规律：

  • \(C[i]\)保存的是以它为根的子树中所有叶节点的和。
  • \(C[i]\)的子节点数量\(lowbit(i)\)
  • \(C[i]\)的父节点为\(C[i+lowbit(i)]\)

4.update 单点更新#

在实际编码中，是没有\(A\)数组的，只有\(C\)数组，数据是保存在\(C\)数组的，但逻辑上的操作是针对A数组，比如获取和更新某个索引位置的元素。

我们知道,\(C\)数组中,父节点是所有子节点的和。当子节点更新时,需要从下至上更新所有关联结点。在更新过程中，也就是需要找到所有父节点。已知 \(C[i]\)的父节点为\(C[i+lowbit(i)]\)，所以每次向上寻找，只需在索引 \(i\) 加上 \(lowbit(i)\)： 

1
2
3
4
while (i <= length) {
  tree[i] += value;
  i += lowBit(i);
}

5.prefix sum 数组前缀和#

查找和的路径有点像单点更新的 逆过程。前i个数的和 \(Sum(i)\)用\(C\)数组可以表示为：

\[ Sum(i) = Sum(i-lowbit(i)) + C[i] \]

代码可以写为： 

1
2
3
4
5
int sum = 0;
while (i > 0) {
  sum += tree[i];
  i -= lowBit(i);
}

reference#

  1. Fenwick Tree
  2. Binary Indexed Trees
  3. 树状数组BinaryIndexedTree
  4. 树状数组学习笔记
  5. 树状数组