why not 哈希索引?#
哈希值是无序的值,既然无序,就 不能进行范围查找,而数据库需要很多大于小于的查找。
如果要进行 排序操作,也不能使用哈希值的哈希索引进行排序(例如不能用uuid做索引,只能做唯一标识,因为也是哈希无序的)。
有些值的 哈希索引是一样的,如果要进行查找,要 逐一比对,相当于全盘扫描。
why not 平衡二叉树?#
平衡二叉树是采用 二分法思维把数据按规则组装成一个树形结构的数据,用这个树形结构的数据 减少无关数据的检索,大大的提升了数据检索的速度;平衡二叉树的数据结构组装过程有以下特定:
- 平衡二叉树是一种 二叉查找树
- 每个结点的左子树的高度减去右子树的 高度的绝对值不超过1
- 空树和左右子树都是平衡二叉树
- 相比红黑树,平衡二叉树比较 适用于没有删除的情况

为什么不能用平衡二叉树: 1. 由于每个子节点最大数量为2,导致 平衡二叉树高度较高,查找次数相对较多。 2. 范围查找时,需要 向上回旋查找(例如查找>=56的数,先找到56,然后向上回旋,找出65和87)
why not B树?#
B 树又叫 平衡多路查找树。一棵m阶的B 树 (注:切勿简单的认为一棵m阶的B树是m叉树,虽然存在四叉树,八叉树,KD树,及vp/R树/R*树/R+树/X树/M树/线段树/希尔伯特R树/优先R树等空间划分树,但与B树完全不等同)的特性如下: 1. 树中每个结点 最多含有m个孩子(m>=2); 2. 除根结点和叶子结点外,其它每个结点 至少有[ceil(m / 2)]个孩子(其中ceil(x)是一个取上限的函数); 3. 若 根结点不是叶子结点,则 至少有2个孩子(特殊情况:没有孩子的根结点,即根结点为叶子结点,整棵树只有一个根节点); 4. 所有 叶子结点都出现在同一层,叶子结点 不包含任何关键字信息(可以看做是 外部接点或查询失败的接点,叶子节点只是没有孩子和指向孩子的指针,这些节点也存在,也有元素。)。 5. 每个非终端结点中包含有n个关键字信息: (n,P0,K1,P1,K2,P2,......,Kn,Pn)。其中: a) Ki (i=1...n)为关键字,且关键字按顺序升序排序K(i-1)< Ki。 b) Pi为指向子树根的接点,且指针P(i-1)指向子树种所有结点的关键字均小于Ki,但都大于K(i-1)。 c) 关键字的个数n必须满足: [ceil(m / 2)-1]<= n <= m-1。
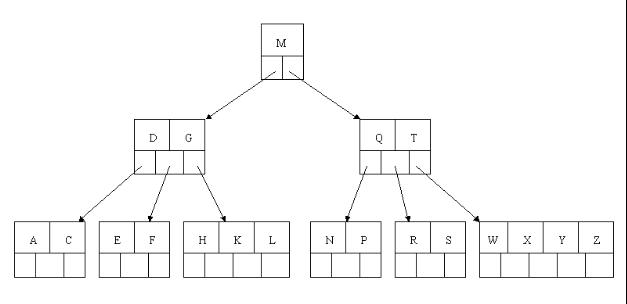
为什么不能用B树: 查找深度明显比平衡二叉树要低,但是范围查找仍然需要 向上回旋查找
why choose B+树?#
B+树是B树的一个升级版,相对于B树来说B+树更 充分的利用了节点的空间,让查询速度更加稳定,其速度 完全接近于二分法查找。为什么说B+树查找的效率要比B树更高、更稳定;我们先看看两者的区别
B树和B+树#
- B+跟B树不同,B+树的 非叶子节点不保存关键字记录的指针,只进行数据索引,这样使得B+树每个非叶子节点所能保存的关键字大大增加;
- B+树 叶子节点保存了父节点的所有关键字记录的指针,所有数据地址必须要到叶子节点才能获取到。所以 每次数据查询的次数都一样;
- B+树叶子节点的关键字 从小到大有序排列,左边结尾数据都会保存右边节点开始数据的指针。
- 非叶子节点的子节点数=关键字数(来源百度百科)(根据各种资料
这里有两种算法的实现方式,另一种为非叶节点的关键字数=子节点数-1(来源维基百科),虽然他们数据排列结构不一样,但其原理还是一样的。Mysql
的B+树是用第一种方式实现);
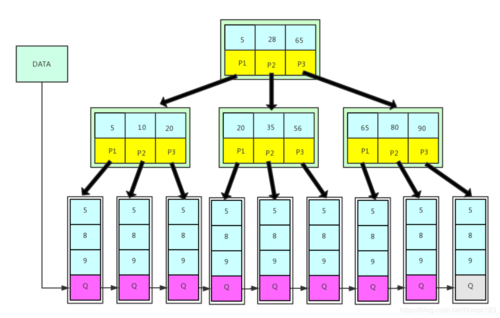
因此,B+树的 查找次数少(树的高度低),范围查找也快(叶子节点通过指针连接)