整数溢出#
c语言中,32位机器的int 长度为32 位,表示的范围: [-2147483648, 2147483647], 超过这个范围就会溢出了。 由于整数溢出现象的存在,程序员需要结合业务场景,谨慎选择数据类型。
而在python中,就没有整数溢出的烦恼。 Python
可以计算十的一百次方,这在其他语言是不可想象的:
1
2>>> 10 ** 100
10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
int 对象#
int 对象在 Include/longobject.h 头文件中定义:
1
typedef struct _longobject PyLongObject; /* Revealed in longintrepr.h */
1
2
3
4struct _longobject {
PyObject_VAR_HEAD /*可变长对象都具有的公共头部*/
digit ob_digit[1]; /*这里存储int的整数值*/
};1
2
3
4
5
6
7#if PYLONG_BITS_IN_DIGIT == 30
typedef uint32_t digit;
// ...
#elif PYLONG_BITS_IN_DIGIT == 15
typedef unsigned short digit;
// ...
#endif
Python 作者为什么要这样设计呢?这主要是 出于内存方面的考量:对于范围不大的整数,用 16 位整数表示即可,用 32 位就有点浪费。
整数对象| 对象大小(16位)| 对象大小(32位) -:-|-:-|-:- 1|24 + 2 * 1 = 26|24 + 4 * 1 = 28 1000000 |24 + 2 * 2 = 28|24 + 4 * 1 = 28 10000000000 |24 + 2 * 3 = 30|24 + 4 * 2 = 32
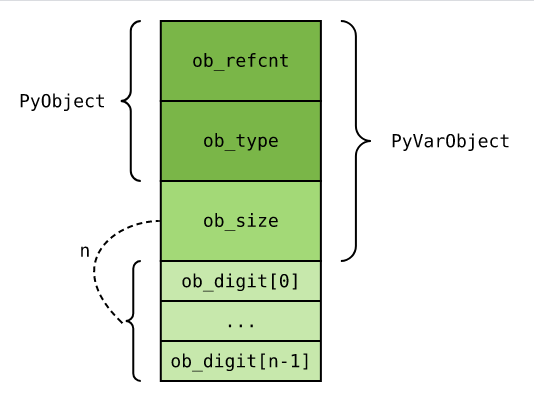
Q:ob_digit 数组长度可能大于1,而为什么在结构体定义中, ob_digit 数组长度却固定为 1?#
由于 C 语言中 数组长度不是类型信息,我们可以 根据实际需要为 ob_digit 数组分配足够的内存,并将其当成长度为 n 的数组操作。这也是 C 语言中一个常用的编程技巧。长度信息在 PyVarObject(PyVarObject比PyObjcet多了个ob_size字段,详细定义可以看[python源码分析] 1.对象)中的ob_size中。
实现大整数#
整数分为 正数 、 负数 和 零 , Python 规定不同整数在 int 对象中的存储方式,要点可以总结为 3 条:
整数 绝对值 根据实际情况分为若干部分,保存于 ob_digit 数组中; ob_digit 数组长度 保存于 ob_size 字段,对于 负整数 的情况,ob_size 为负(这里可以说就很精妙了); 整数 零 以 ob_size 等于 0 来表示,ob_digit 数组为空; 接下来,我们以 5 个典型的例子详细介绍这几条规则:
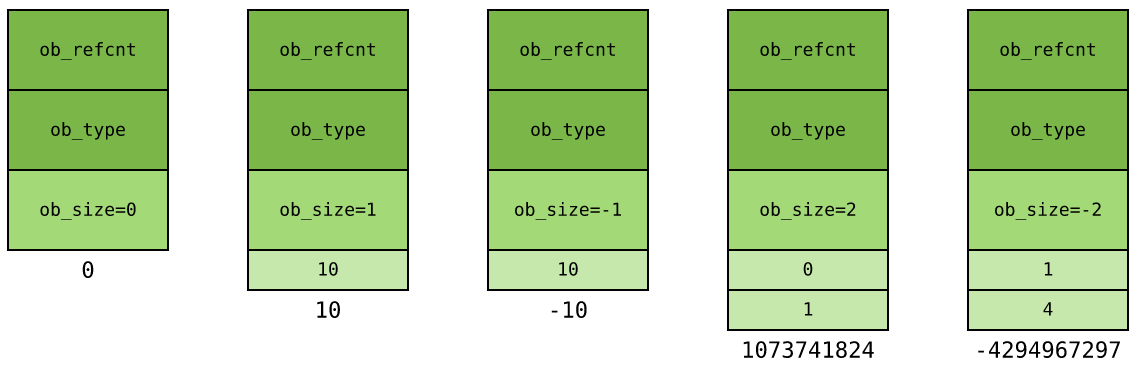
- 对于整数 0 , ob_size 字段等于 0 , ob_digit 数组为空,无需分配。
- 对于整数 10 ,其绝对值保存于 ob_digit 数组中,数组长度为 1 , ob_size 字段等于 1 。
- 对于整数 -10 ,其绝对值同样保存于 ob_digit 数组中,但由于 -10 为负数, ob_size 字段等于 -1 。
- 对于整数 1073741824 ( 2 的 30 次方),由于 Python 只使用 32 整数的后 30 位,因此 需要另一个整数才能存储,整数数组长度为 2 。绝对值这样计算:\(2^{30}*1+2^0*0=10737418242\)
- 对于整数 -4294967297 (负的 2 的 32 次方加 1 ),同样要长度为 2 的 ob_digit 数组,但 ob_size 字段为负。绝对值这样计算:\(2^{30}*4+2^0*1=42949672972\)
为什么 Python 只用 ob_digit 数组整数的后 30 位?#
这跟 加法进位有关。如果全部 32 位都用来保存绝对值,那么为了保证加法不溢出(产生进位),需要先强制转换成 64 位类型后在进行计算。但 牺牲最高 1 位后,加法运算便不用担心进位溢出了。那么,为什么 Python 牺牲最高 2 位呢?应该是 为了和 16 位整数方案统一起来:如果选用 16 位整数作为数组, Python 则只使用其中 15 位。
小整数静态对象池#
小整数对象池在 Objects/longobject.c 中实现,关键代码如下:
1
2
3
4
5
6
7
8
9/*小整数池的范围通过宏来定义的, 默认是-5-257,我们可以通过修改此处的宏来调整小整数池的大小, 但是需要对python进行重新编译*/
#ifndef NSMALLPOSINTS
#define NSMALLPOSINTS 257 /*该宏规定了对象池 正数个数 (从 0 开始,包括 0 ),默认 257 个*/
#endif
#ifndef NSMALLNEGINTS
#define NSMALLNEGINTS 5 /*该宏规定了对象池 负数个数 ,默认 5 个*/
#endif
static PyLongObject small_ints[NSMALLNEGINTS + NSMALLPOSINTS]; /*一个整数对象数组,保存预先创建好的小整数对象*/
如果在[-5,
257)范围内,会直接返回存于small_ints的对象,所以小整数只会存在一个实例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15// longobject.c
static PyObject *
get_small_int(sdigit ival)
{
PyObject *v;
assert(-NSMALLNEGINTS <= ival && ival < NSMALLPOSINTS);
v = (PyObject *)&small_ints[ival + NSMALLNEGINTS];
Py_INCREF(v);
#ifdef COUNT_ALLOCS
if (ival >= 0)
quick_int_allocs++;
else
quick_neg_int_allocs++;
#endif
return v;
至于为什么选择静态缓存从 -5 到 256 之间的小整数,主要是出于某种 权衡 :这个范围内的整数使用 频率很高 ,而缓存这些小整数的 内存开销相对可控 。很多程序开发场景都没有固定的正确答案,需要根据实际情况平衡利弊。
理解了静态对象池,如下现象就很好理解了:
1
2
3
4
5
6
7
8
9>>> a = 1 + 0
>>> b = 1 * 1
>>> id(a), id(b)
(4408209536, 4408209536)
>>> c = 1000 + 0
>>> d = 1000 * 1
>>> id(c), id(d)
(4410298224, 4410298160)
由于整数对象是 不可变对象 ,任何整数运算结果都以新对象返回,而对象创建销毁开销却不小。为了优化整数对象的性能, Python 在启动时将使用 频率较高 的小整数预先创建好,这就是 小整数缓存池 。默认情况下,小整数缓存池缓存 从 -5 到 256 之间的整数。
数学运算#
根据我们在 PyTypeObject 中学到的知识,对象的行为由对象的 类型 决定。因此,整数对象 数学运算的秘密藏在整数类型对象中。在 Objects/longobject.c 中找到整数类型对象( PyLong_Type ),其定义如下所示:1 | PyTypeObject PyLong_Type = { |
1 | static PyNumberMethods long_as_number = { |
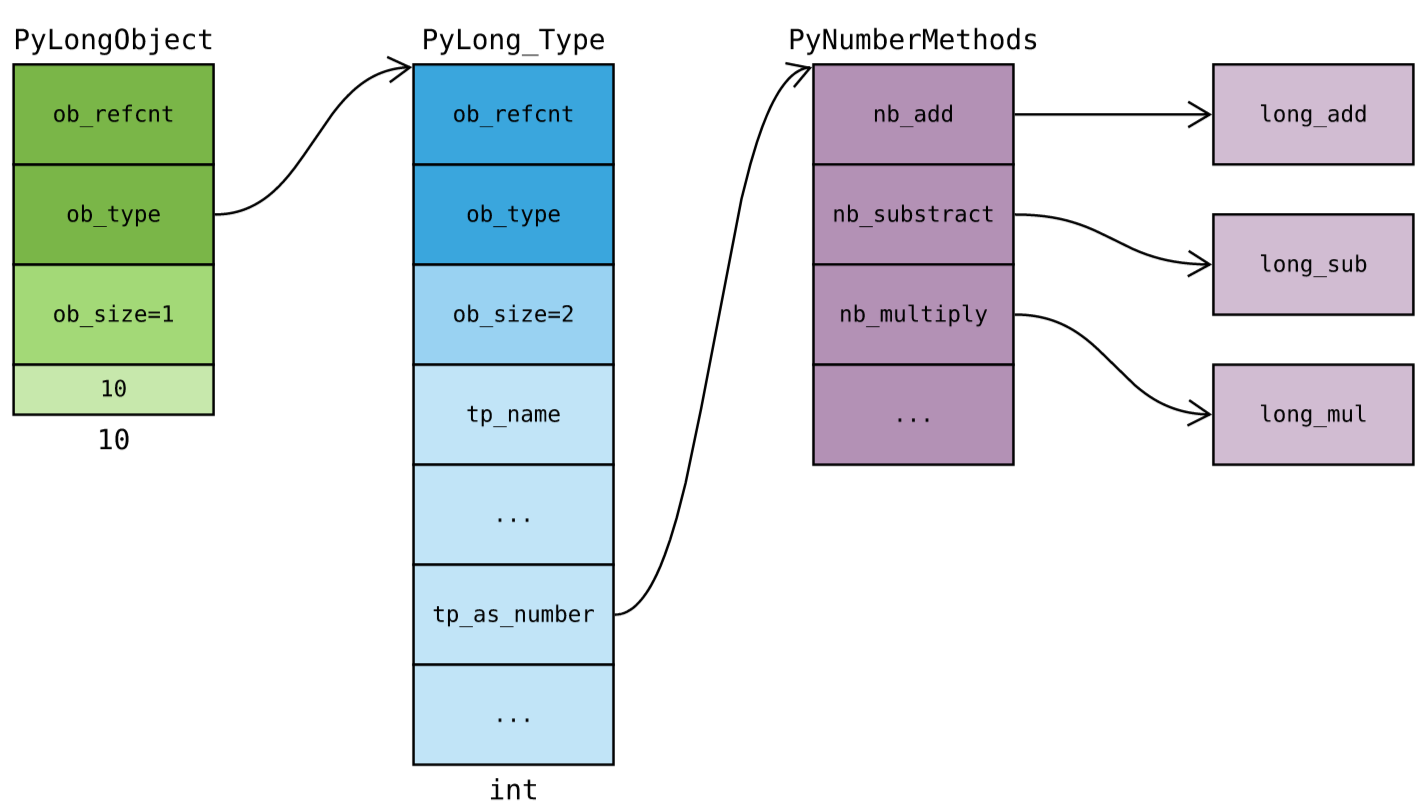
加法#
如何为一个由数组表示的大整数实现加法?问题答案得在 long_add
函数中找,该函数是整数对象 加法处理函数 。我们再接再厉,扒开 long_add
函数看个究竟(同样位于 Objects/longobject.c ):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38static PyObject *
long_add(PyLongObject *a, PyLongObject *b)
{
/*定义变量 z 用于临时保存计算结果*/
PyLongObject *z;
CHECK_BINOP(a, b);
/*
如果参与运算的整数对象底层数组长度均不超过 1 ,直接用 MEDIUM_VALUE 宏将整数对象转化成 C 整数类型进行运算,
性能损耗极小。满足这个条件的整数范围在 -1073741823~1073741823 之间,足以覆盖程序运行时的绝大部分运算场景
*/
if (Py_ABS(Py_SIZE(a)) <= 1 && Py_ABS(Py_SIZE(b)) <= 1) {
return PyLong_FromLong(MEDIUM_VALUE(a) + MEDIUM_VALUE(b));
}
if (Py_SIZE(a) < 0) {
if (Py_SIZE(b) < 0) {
/*如果两个整数均为 负数 ,调用 x_add 计算两者绝对值之和,再将结果符号设置为负( 16 行处)*/
z = x_add(a, b);
if (z != NULL) {
assert(Py_REFCNT(z) == 1);
Py_SIZE(z) = -(Py_SIZE(z));
}
}
/*如果 a 为负数, b 为正数,调用 x_sub 计算 b 和 a 的绝对值之差即为最终结果*/
else
z = x_sub(b, a);
}
else {
if (Py_SIZE(b) < 0)
z = x_sub(a, b);
else
/*如果两个整数均为正数,调用 x_add 计算两个绝对值之和即为最终结果*/
z = x_add(a, b);
}
return (PyObject *)z;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43static PyLongObject *
x_add(PyLongObject *a, PyLongObject *b)
{
/*取ob_size的绝对值*/
Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
/*用变量z 临时存储计算结果*/
PyLongObject *z;
Py_ssize_t i;
/*临时进位*/
digit carry = 0;
/* Ensure a is the larger of the two: */
if (size_a < size_b) {
/*如果 a 数组长度比较小,将 a 、 b 交换,数组长度较大的那个在前面*/
{ PyLongObject *temp = a; a = b; b = temp; }
{ Py_ssize_t size_temp = size_a;
size_a = size_b;
size_b = size_temp; }
}
/*创建新整数对象,用于保存计算结果(注意到长度必须比 a 和 b 都大一,因为可能有进位)*/
z = _PyLong_New(size_a+1);
if (z == NULL)
return NULL;
/*遍历 b 底层数组,与 a 对应部分相加并保存到 z 中,需要特别注意进位计算*/
for (i = 0; i < size_b; ++i) {
carry += a->ob_digit[i] + b->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
/*遍历 a 底层数组剩余部分,与进位相加后保存到 z 中,同样需要特别注意进位计算*/
for (; i < size_a; ++i) {
carry += a->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
/*将进位写入 z 底层数组最高位单元中*/
z->ob_digit[i] = carry;
/*去除计算结果 z 底层数组中前面多余的零,因为最后的进位可能为零*/
return long_normalize(z);
}